Frequency Response Analyzer
Moku:Lab’s Frequency Response Analyzer (FRA) drives a swept sine wave on Moku:Lab‘s outputs and simultaneously measures the received signal amplitude (or power) and phase on Moku:Lab’s inputs. This can be used to measure the transfer function of a system or device under test and subsequently create a plot of amplitude and phase vs frequency, commonly referred to as a Bode plot.
FRA : Power units
In the first part of this application note series [1], we discussed the dBm power measurement of a 1 Vpp sine wave-driven out from Moku:Lab’s output and looped back into a Moku:Lab input.
We determined that this 1 𝑉pp, driven across the 50 Ω input of Moku leads to a power measurement:

We then used this power ratio to accurately measure resistive impedance.
Inductance
Two-port measurement
For this example, we will measure a known inductor; a Wurth electronics part #7447021. This is a 100 µH inductor, specified at 10 kHz with a ± 20% tolerance.

Table 1: Inductor specification from datasheet [2]
For a two-port measurement; we use the first and second Moku:Lab inputs as shown in Figure 2; this
allows accurate measurement, allowing for the inductive loading on the Moku:Lab swept sine output.
Figure 1: Moku:Lab measurement setup
The equivalent circuit, showing Moku:Lab’s input impedances, is shown in Figure 2
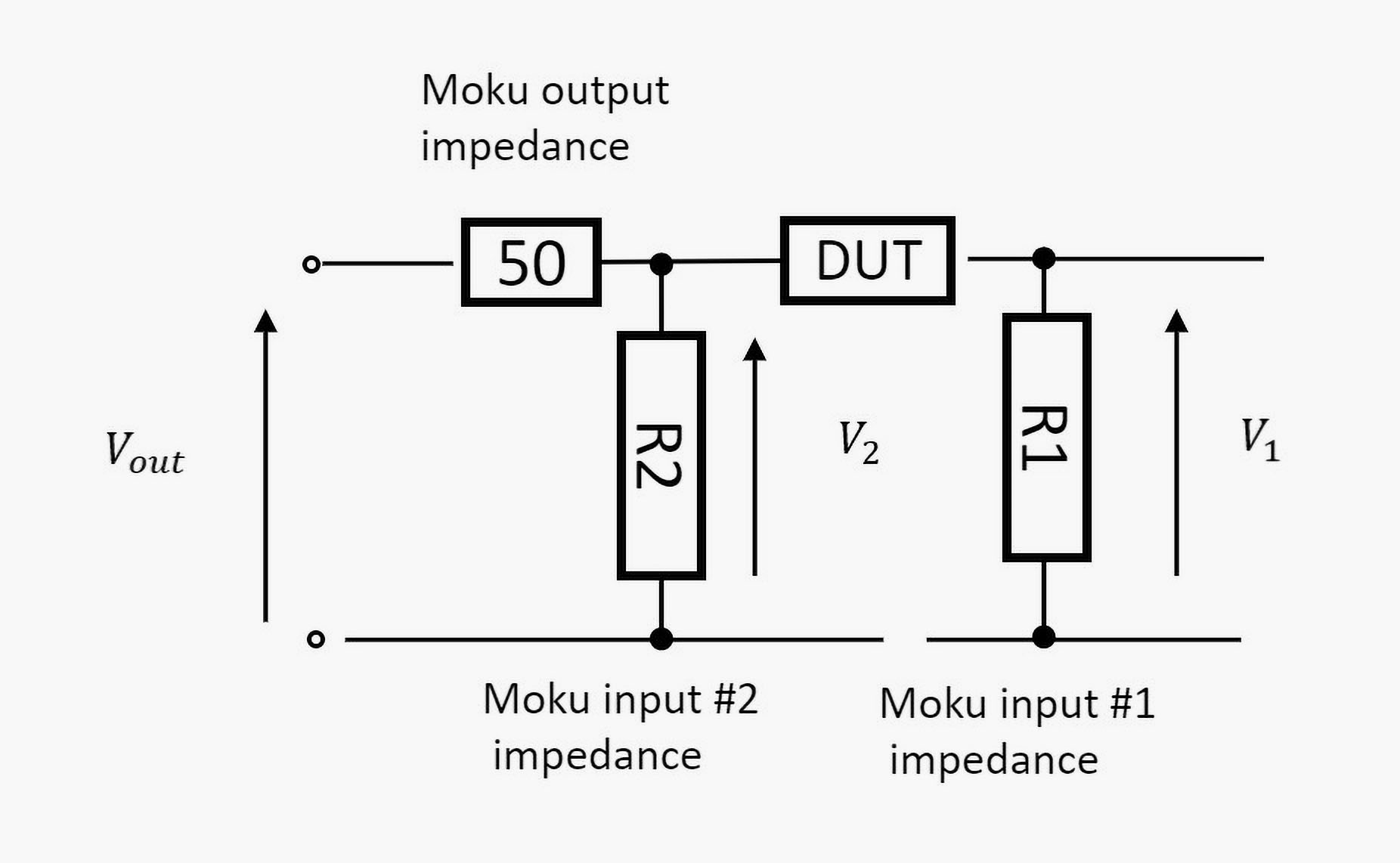
Figure 2: Two-port equivalent circuit
R1 and R2 are the input impedances (50 Ω); the DUT (device under test) is the inductor.
Moku:Lab’s Frequency Response Analyzer will allow us to determine the phase of V1 vs V2 across frequency, as well as the magnitudes.
Calculation
Basic circuit theory tells us that the inductor presents an inductive reactance and that this reactance and Moku:Lab’s 50 Ω resistive input impedance can be represented as a phasor diagram (Figure 3)
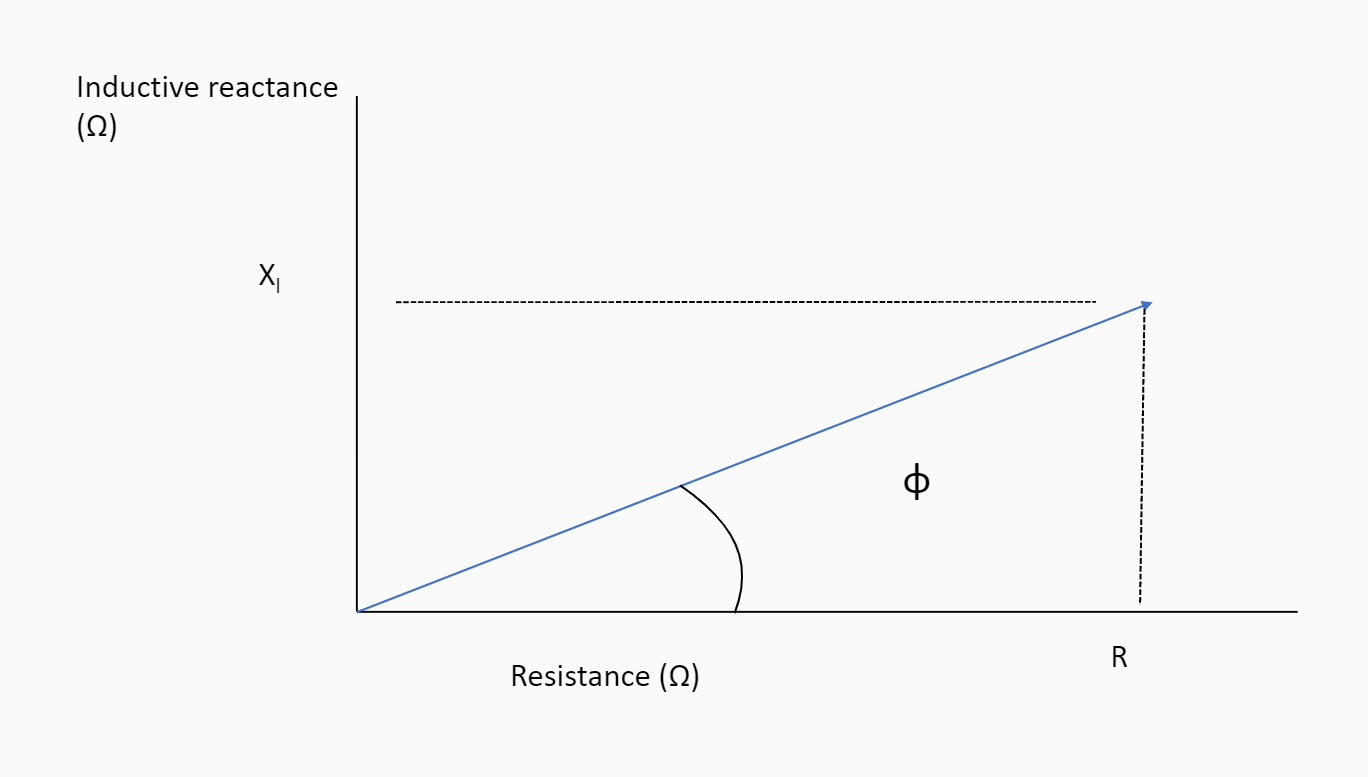

Figure 3: phasor chart of impedance
So, we can determine the inductance L if we measure the phase ∅ at frequency 𝑓.
Measurement setup and result

Figure 4: Moku:Lab bench setup
Figure 4 shows the Moku:Lab bench setup; it takes just moments to setup the Frequency Response Analyzer instrument on Moku:Lab’s iPad app and to produce the plots of magnitude and phase vs frequency. The plots on the iPad are then shared by tapping the ‘cloud’ button. Screenshots and high resolution .CSV formatted data are exported to MyFiles, SD card, or Email. In this case, we shared the data to a Dropbox folder and Figure 5 is the resulting screenshot.
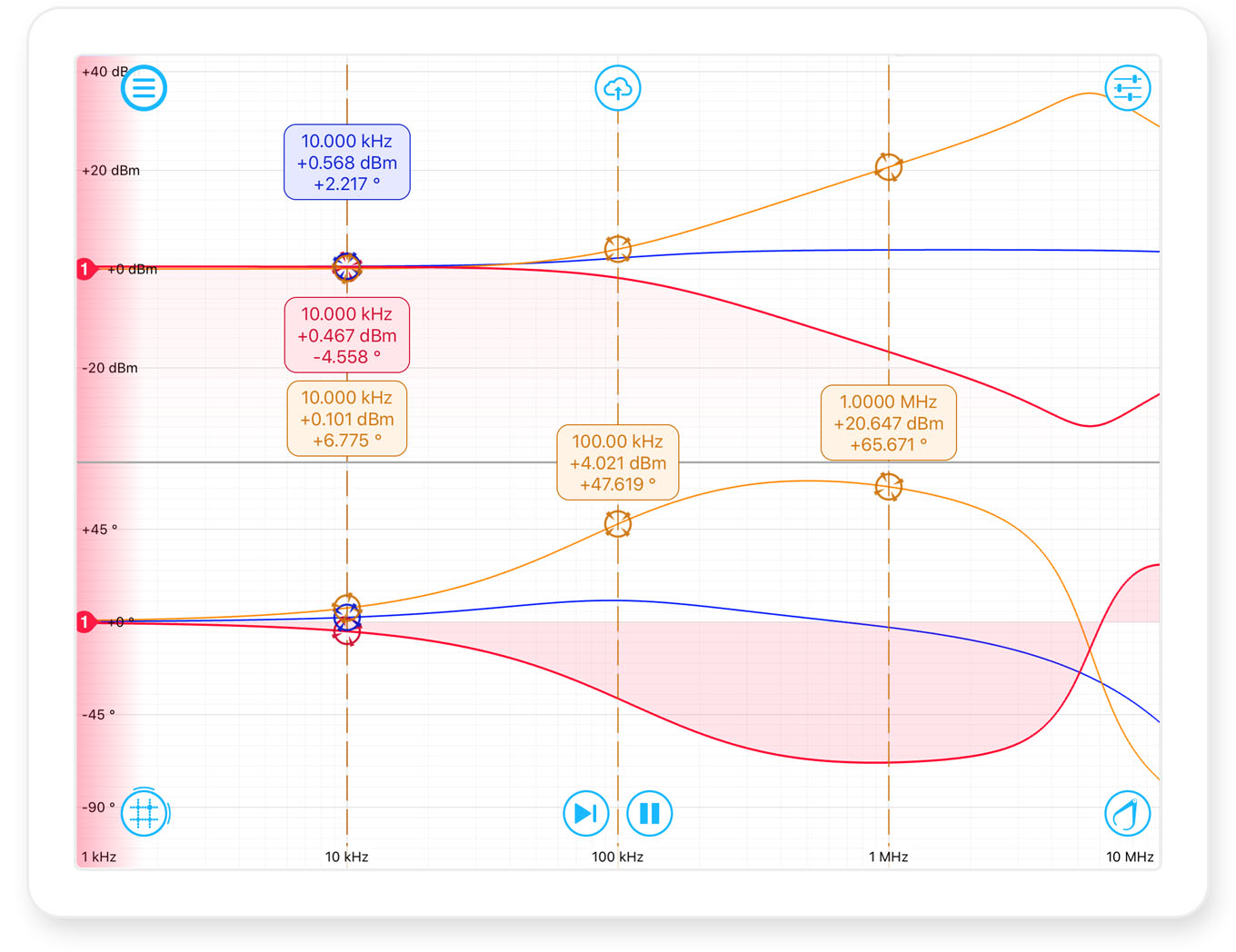
Figure 5: Frequency Response Analyzer sweep 100 μH
The swept sine is generated from 1 kHz to 10 MHz on Moku:Lab’s output channel 1. The blue trace shows Moku:Lab’s channel 2 (V2), while the red trace is Moku:Lab’s channel 1 (V1). The Moku:Lab math channel is in orange and is configured to show (ch2 ÷ ch1). Several cursors have been added to measure the phase and magnitude at 10 kHz, 100 kHz and 1 MHz.
The orange math channel cursors allow us to quickly see the phase difference at our 10kHz frequency of interest to be ∅ = 6.775°.
From (1) we calculate 𝑋L= 5.94 Ω
And from (2) the inductor value L = 94.5 μH
This is well within the specification of 100 µH ± 20%.
While the inductor is specified at 10 kHz, we can also take our measurements from figure 5 at 100 kHz, where ∅= 47.619°. Again applying Eq(2); this gives L = 87.2 µH. This is quite reduced but the usual behavior of a real-world coil inductor.
Since we used Moku:Lab’s app to save the high resolution FRA magnitude and phase data to a .CSV file via Dropbox, we can rapidly import this into Excel and, using Eq (2), produce a plot of inductance (blue) and phase (green) vs frequency:
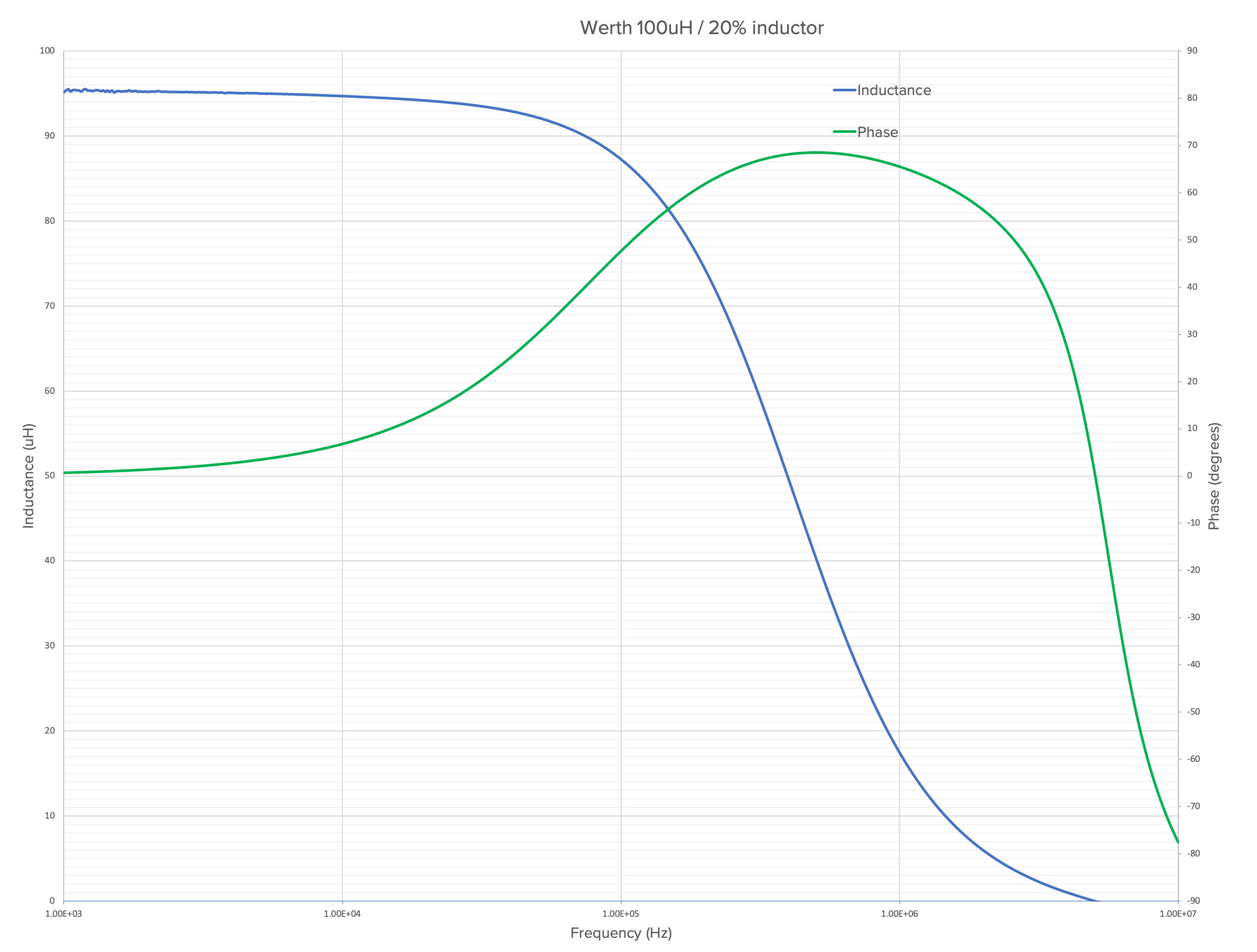
Figure 6: Inductance & phase vs frequency
This clearly shows that above 100 kHz, the inductance falls off steadily until at around 5 MHz, the inductance is effectively zero.
This occurs because a real-world practical coil inductor is not a perfect inductor, but rather it has some resistance and capacitance. The equivalent circuit is actually as shown in Figure 7
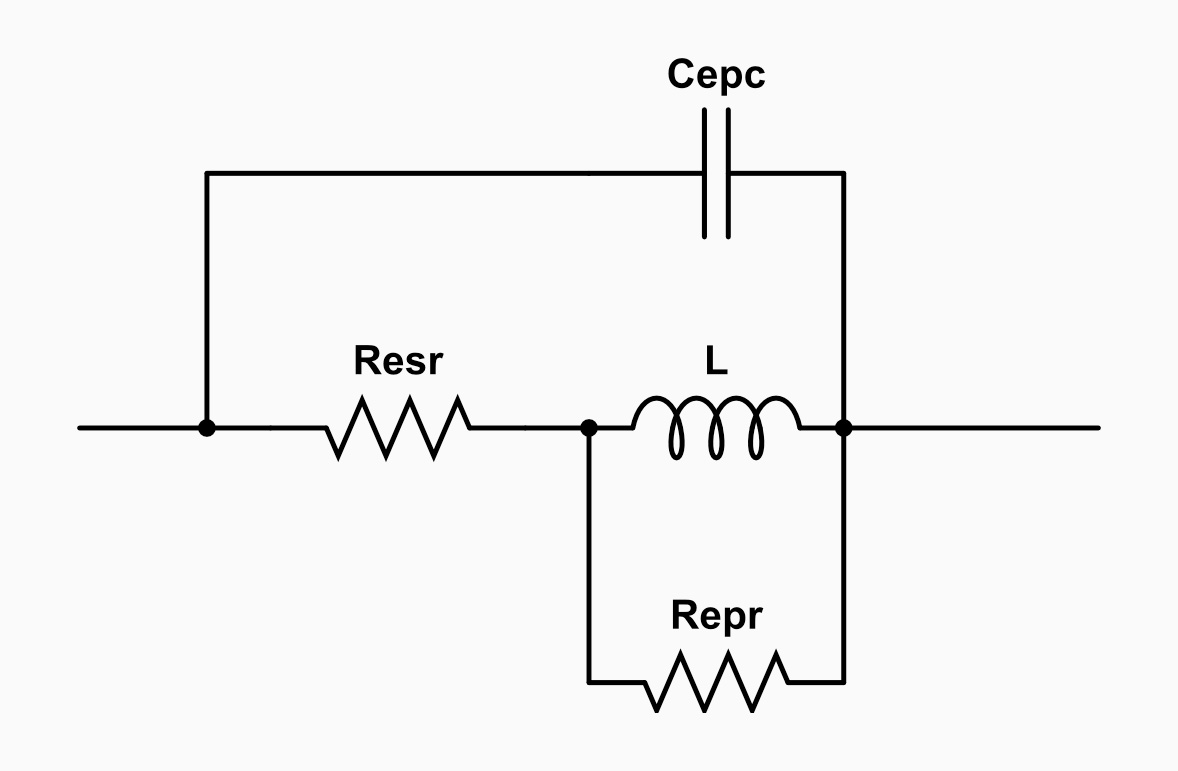
Figure 7: Inductor equivalent circuit
A perfect inductor has impedance that linearly rises with frequency. But a real-world inductor has an effective parasitic capacitance in parallel (Cepc) together with resistive elements Resr and Repr. Resr is sometimes quoted in datasheets as DC resistance and is the resistance of the wire coil; Repr is effective parallel or AC resistance and Cepc is parallel capacitance due to proximity of the wire coils.
Thus, there is a resonance frequency determined by:
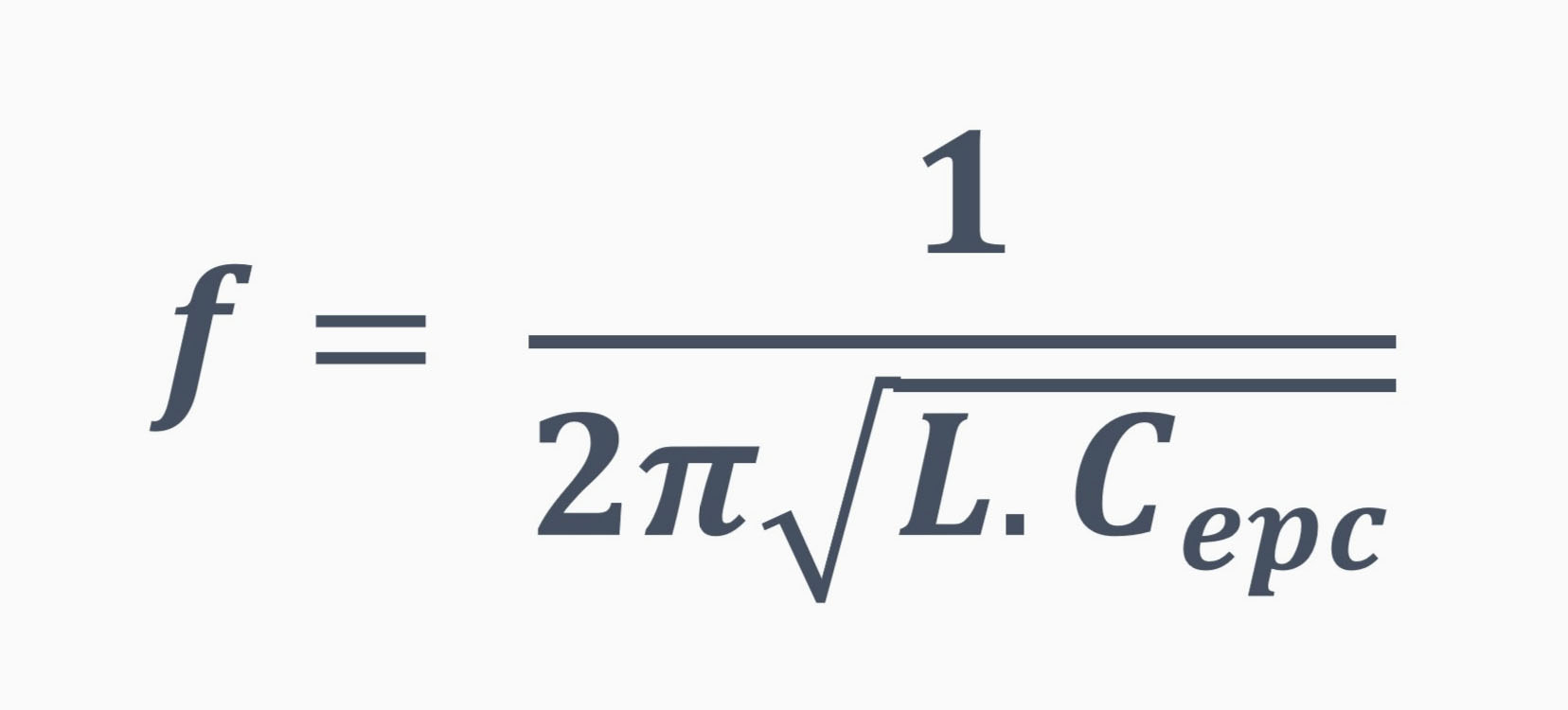
Again referring to [2], we see that the inductor has a typical impedance characteristic and this is reproduced in Figure 8, showing resonance peak at around 5 MHz.
![Figure 8: Wurth inductor typical impedance: ref [2]](https://dev.liquidinstruments.com/wp-content/uploads/2020/03/12-FIG1.jpg)
Figure 8: Wurth inductor typical impedance: ref [2]
Because Moku:Lab makes it so straightforward to share the FRA data to a .CSV via Dropbox, we can readily use Excel to provide a plot of magnitude impedance vs frequency, as shown in Figure 9
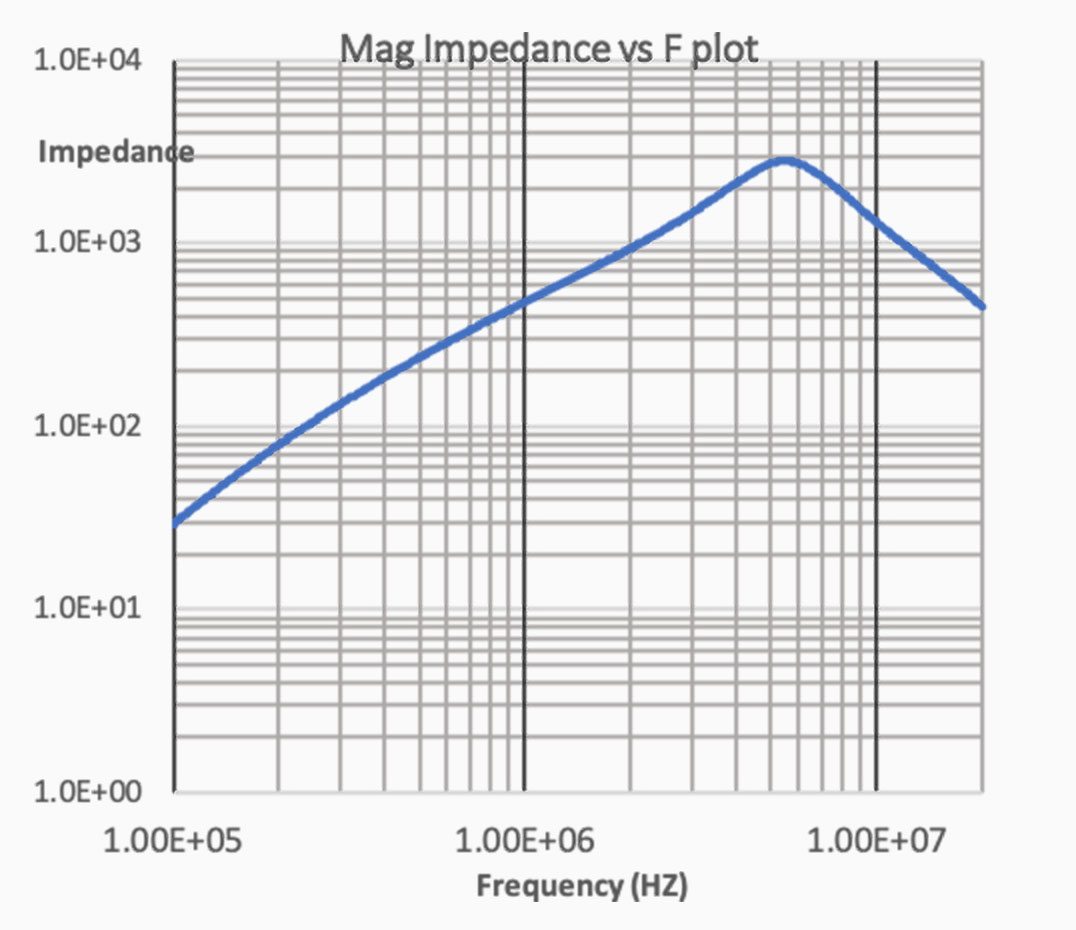
Figure 9: Moku:Lab measured impedance
The resonance, as measured is slightly above 5MHz and the characteristics of the measurement are closely in line with the typical performance of Figure 8, taken from the manufacturer’s datasheet.
Summary
Moku:Lab’s Frequency Response Analyzer can be readily used to accurately measure the inductive impedance of component over frequency.
The results were shared via a .CSV file and Dropbox with a few taps of Moku:Lab’s iPad app. Excel was used to plot both inductance & phase vs frequency together with impedance vs frequency.
The calculated impedance at specified 10kHz matches the component specification. Additionally, the plotted impedance vs frequency closely matched the manufacturers ‘typical’ chart up to 20 MHz.
References
[1] A guide to measuring impedance with Mok:Lab’s Frequency Response Analyzer (Part 1)
[2] Wurth Electronics 100uH coil inductor data sheet, https://www.we-online.de/katalog/datasheet/7447021.pdf
[3] Moku:Lab FRA user manual
Questions or comments?
Please contact us at support@liquidinstruments.com



